ἡ ἀλήθεια ἐλευθερώσει ὑμᾶς. VERITAS VOS LIBERABIT. 真理将使你们得自由。
数学是什么
廖源 数学博士
(PhD,美国佛罗里达大学统计学专业博士)
【作者简介:廖源,中国科技大学数学与应用数学专业本科,中国科学院研究生院概率统计专业硕士(导师为陈希孺院士),美国佛罗里达大学统计学专业博士(导师为Dr. Andrew Rosalsky教授),孔亚学园创始导师团导师】
1. 数学之于我们,既熟悉又陌生。生活中充斥着与之相关的活动,但我们是否思考过「数学是什么」「为什么要学习数学」「如何学习数学」?每个人都可以且应该问「数学是什么」。一个第一次上数学课的孩子应该问这个问题,因为他对这个世界充满好奇。数学老师需要思考这个问题,因为这是老师的基本职责。理工科的科研工作者更需要问这个问题,因为这是他的工作对象或科研工具。文科的科研工作者也要问这个问题,因为数学是人文精神的产物。每一个受过正规教育成年人都应该问这个问题,这既是对自己负责,是对后代负责,更是对社会和国家负责。数学,作为人类文明的一部分,也作为我们日常生活的一部分,我们有责任去思考「数学是什么」。一个人对「数学是什么」理解越深刻,就会越发清楚地明白「为什么要学习数学」,同时也更清楚「如何学习数学」。
2. 「数学是什么」没有标准答案,不同的人有不同的理解,同一个人在不同的人生阶段对其理解也不同。可能考虑到学术定义的一般性,词典和教科书给出的大部分的解释让人望而生畏或不知所云。最常见的定义是「数学是关于数、形、关系,以及变化的学问」。现如今数学已然发展为一种远离大众的、只有数学工作者才能参与其中的、颇难定义的智力活动。不过我们可以尝试一种「放之四海而皆准」的方法,那就是探索数学的历史,即其时空演变。
3. 古往今来,「数学」一词的含义有如旧瓶装新酒,不断地随着人类文明的发展而演变。最初的数学是人类日常生活需要的一部分:牧羊人放牧后关心羊群是否数目有变,部落间的物品交易需要清点库存,武装冲突后需要计量人员伤亡,宗教仪式上召唤特定数目的参加者上场等等。人类在寻找差异的同时,也发现了共性,即对于「数」的认知。「数」的概念的发展是一个漫长、渐进、且非线性的过程,时间或许可以上溯到大约30万年前,也就是人类开始使用火的时候。与「数」的概念同样古老的是「形」的概念,新石器时代的陶器、编织和编筐等日常生活用品上的图画和图案暗示了初等几何学的萌芽。在最近的不到6000年里,人类才以文字的形式记录下他们的思考,可见「数」与「形」作为数学的起源,比书写古老的多得多,也更具神秘色。原始人类没有在数学上没有突破性进展,这种情况一直到公元前3000年左右古埃及和古巴比伦。我们从古巴比伦人的石板上的楔形文字了解其对数学的贡献,而古埃及人留给我们的是莎草纸文书。公元前800年,世界的文明中心逐渐转移至古希腊,直至古罗马时期,数学逐渐成为一门真正的学科。古希腊人对数学做出了巨大贡献,古罗马人太注重实际,虽然继承了希腊文明,但没有推动数学发展。其后印度人和阿拉伯人有一定贡献,到了中世纪约从公元400年起到1100年,欧洲的基督教主要关注精神世界,对物理世界缺乏兴趣,这段时间数学进展缓慢。公元1100年左右,欧洲人通过贸易和旅游开始从阿拉伯和东罗马的拜占庭接触古希腊著作,大批古希腊和阿拉伯著作被译成拉丁文。到了公元1400年文艺复兴时期,欧洲的政治、思想、和文化的巨大变革使得数学活动蓬勃兴起。截至公元1600年,欧洲的科学家无疑地注意到数学在自然科学中的重要性,开始了科学的数学化。到了17世纪,数学开始研究运动和变化,物理和数学交相呼应,都开始了根本性变革。大约18世纪中期之后,数学家开始关注数学本身,特别是重新审查数学基础,古希腊严谨的演绎证明卷土重来,纯粹数学和应用分道扬镳。分离也预示着再度结合,从20世纪初至今,主流理论间不断碰撞出新的支流,理论与应用相互促进、互为养分,毫不夸张地说近一百年数学的发展相当戏剧化,充满了不确定性。
4. 上段文字仅给出一个数学史的极简时空排序(没有列出中国),是数学的外在历史,它和人类思想的时空演变交相呼应。这并不是巧合,因为数学是人类思想独一无二的组成部分,数学史也是思想史的一部分。思想史有别于其他历史的最独特之处在于,外在时间框架下的思想流变可以内化于人的意识,从而不依赖于时间线性(逻辑的一大特点就是独立于外在时间的普遍性和一般性)。时间不能倒流,具体的历史事件无法重演,但是我们可以在思维中去重现、思考和延申从古至今已知的任何思想,包括数学。我们可以把外在时间上的数学史内化为思维意识中的数学,不同时间的数学叠加在一起同时呈现于思维意识。例如,虽然人类形成「数」和「形」的概念可能比使用火还要早,但这不妨碍现代人理解原始人的思维意识;虽然历史上「0」晚于其他自然数出现,但是我们的思维意识中只有「0、1、2、…」这样的排序,几乎没人认可「1、2、…、0」。这也决定了数学的独一无二,即其发展的连续性和拓展性。在数学中,一般先要定义其研究对象,或者以无定义的公理系统开始(这点刚好与物理学相反)。数学是累积的学科,它的发展不存在推翻,只有拓展,2000多年前的定理至今依然有效。它好比一幅图景,不断地更高、更宽、更美丽、更宏伟,它的过去「传承」于现在和将来。从这点看数学接近人文学科,因为人文学科的重要本质之一就是「传承」。
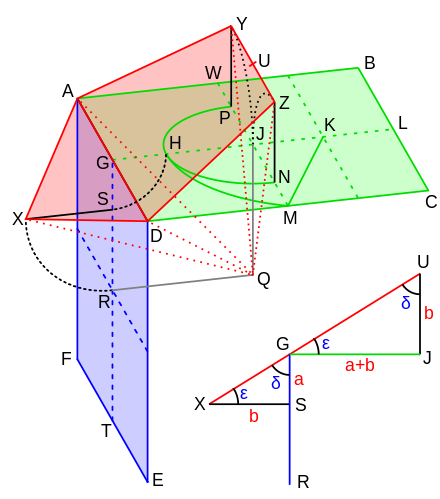
5. 30万年前的人类就有了概念思维。感知和发现事物的共性是我们与生俱来的能力,概括事物的共同点并用语言符号表达是人的概念思维能力的具体实现,即下图中的「语义三角形」(此处不具体阐释“语义三角形”理论,陈庆老师的论文有详细的介绍和讨论,建议大家参考)。
数学的基本单位是概念,数学的根本任务是形成和理解概念,以及发现概念之间的关系,并用文字和符号表达出来。与数学类似,哲学考量的是「本体」「知识」「正义」「道德」「伦理」等概念,物理学关心的是「物质」「质量」「能量」「时间」「空间」等概念。可见哲学、数学、物理学都是人类理智的不同的工作领域,但是它们之间有着千丝万缕的关系(在古希腊,科学和哲学是同一个东西)。当然还有宗教学、法学、宇宙学、生物学、医学等等,都是人类理智对人自身、社会、自然,以及三者间关系的理解。
退后一步看,「语义三角形」的三个「顶点」——符号世界(A)、思维世界(B)、实在世界(C)——的交织互动是产生知识的根本机制。举例来说,物理学是用数学语言(A)表现的对自然(C)的本源和规律的概括思考(B);哲学从一开始的关注实在世界(C),到探求思维(B)如何理解世界(C),再到语言学(A)的转向,也没有跳出这个框架。可以说理解「语义三角形」是认识我们自身的根本出发点,我们无时不刻不在这个三角形中翻腾穿梭,这是人与生俱来的本性使然。
6. 「数学是什么」是一个没有「标准答案」的问题,重要的不是「答案」,而是思考。「纸上得来终觉浅,绝知此事要躬行」,没有实践的「躬行」就没有纸上的「得来」。至于说「为什么要学习数学」,这是一个显而易见的问题。仅仅为了考试或其他外在的功利性目的而学习数学简直是舍本逐末。一个从人类文明初始就存在的、蓬勃发展至今的学科,一个密切联系人的内在精神世界和外在自然和社会的学科,难道不值得每个人认真学习么?
7. 如何学习数学?「问渠哪得清如许,唯有源头活水来」。首先要「正本清源」。前面已经追本溯源地介绍过数学是「语义三角形」中的人的理智思维(B)和实在世界(C)互动的产物。人是C中的存在,B是人与生俱来的能力,二者的存在都不以人的意志为转移。所以,「学习数学」其实不是一个「学习」的过程,而是「发现」「认识」和「培养」自我的过程,这也是「教育」的本质。其次要系统地、整体地看待数学教育。前面说过,数学是概念思维的产物「之一」,那么自然要问概念思维还能做什么?人的精神世界除了概念思维还有什么?运用概念思维的同时其他情感或情绪因素是否参与?如果有,那么是如何参与的、作用是什么?任何事物我们都不能孤立地看待,要把数学思维的培养嵌入到人的成长和生活中去综合考量,充分重每个人的天性和成长规律,还有什么比完善的人格和自我教育的能力更重要的。最后,数学教育,乃至教育本身,无一不是实践的智慧,需要家庭、学校和社会的有机结合以及长期不屑的努力。
后记
陈庆博士,吾师、亦友。4月28日,陈师与我于西南大学食堂共进早餐时,建议我写些比较中美高等数学教育的文字,准备发表于他创办的公众号平台。陈师约稿到现在几近半年,实在不知从何写起。毕业至今我不再从事学术工作,如今仅作为业余的学术爱好者,分享些许个人感受,也算不枉陈师的信任和委托。
此文形成于这半年的碎片时间。为便于读者理解,我尽量使用通俗的语言,避免任何专业术语,以期在通俗和准确之间达到合适的平衡。为避免长篇大论和陷入教条,文中很多要点一带而过、浅尝辄止。总之,不妥之处在所难免,还请大家批评和谅解。不管怎样,能给大家带来些许启示或思考,我就很欣慰了。
2021年10月6日于北京